
Poincaré-Vermutung
Wenn es wie eine Kugel aussieht und sich wie eine Kugel anfühlt, ist es dann wirklich eine Kugel?
In der Wissenschaft geht es oft darum, Naturphänomene und Objekte zu verstehen, indem man herausfindet, wann diese ähnlich sind und wann nicht. Chemikerinnen und Chemiker teilen die chemischen Elemente in einem Periodensystem ein und Biologinnen und Biologen nutzen die beobachtbaren Eigenschaften von Pflanzen und Tieren, um die verschiedenen Spezies zu beschreiben. In einem ähnlichen Sinne sind manche Mathematikerinnen und Mathematiker daran interessiert, herauszufinden, wann bestimmte Formen sich ähnlich oder komplett verschieden sind.
Mathematik umgibt uns überall – in einer Bäckerei, der Küche, einem Spielplatz…
Hier sind ein paar alltägliche Gegenstände, die wir intuitiv nach bestimmten strukturellen Eigenschaften einteilen können:

Group 0

Group 1

Group 2

Group 3
Alle Objekte in den Bilder befinden sich im dreidimensionalen Raum. Wenn wir sie als gefüllt ansehen (uns den Apfel also mit seiner Schale und dem Fruchtfleisch vorstellen), dann sind dies selber auch dreidimensionale Objekte. Wir wollen uns heute aber nur den Rand eines solchen Objekts anschauen (nur die Schale des Apfels), das ergibt eine zweidimensionale Fläche im dreidimensionalen Raum. Hier ist nun ein kleines Rätsel für dich:
Die Anzahl ihrer “Löcher”! Die Objekte in Gruppe 0 haben null Löcher, die Objekte in Gruppe 1 haben ein Loch, und so weiter.
Die intuitive Idee, dass Objekte “Löcher haben” wurde von Henri Poincaré zum ersten Mal mathematisch präzise formuliert. Seine Arbeit hatte einen starken Einfluss auf das mathematische Gebiet der Topologie, das sich allgemeiner mit dem Raum und den darin enthaltenen Punkten beschäftigt (Topologie ist vom griechischen Word “τόπος”=”Ort” abgeleitet).
Diese präzisere mathematische Charakterisierung der Gruppe 0 nutzt die folgende Definition der “Lasso-Eigenschaft”.
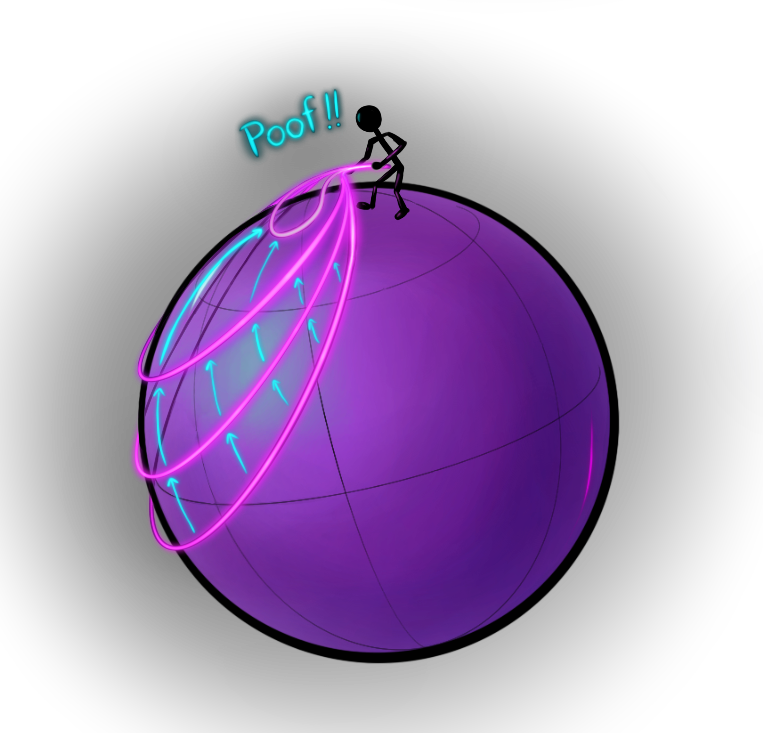

Lasso-Eigenschaft: Wir stellen uns vor, wir binden ein elastisches Band in einer Schlaufe entweder um eine Sphäre (die Oberfläche von einem Ball) oder um einen Torus (die Oberfläche von einem Donut), so wie man es in den Illustrationen links sehen kann.
Wir sehen, dass man man auf der Sphäre das Band immer zusammenziehen kann, so dass es von der Sphäre rutscht. Auf dem Torus dagegen können wir das Band so darumbinden, dass es nicht vom Torus abgenommen werden kann (außer wir zerschneiden den Torus oder zerreißen das Band).
Allgemeiner gilt sogar, dass sich alle zweidimensionalen Formen unterscheiden lassen, indem wir die Anzahl der Löcher betrachten – ebenso wie bei den Beispielen von Formen, die wir oben betrachtet haben. Für Mathematikerinnen und Mathematiker ist das sehr zufriedenstellend, da wir sogar jedes zweidimensionale Objekt so verformen können, dass es eine bestimmte Form (mit der richtigen Anzahl Löcher) hat wie in den vorigen Beispielen. Topologisch betrachtet, sind ein Torus und ein Becher also gleich.

Verlassen wir nun die zweidimensionale Welt…
Können wir auf eine ähnliche Weise auch kompliziertere Formen verstehen, zum Beispiel die Formen von dreidimensionalen Objekten? Wie sehen denn überhaupt dreidimensionale Objekte aus? Hier ist ein Beispiel eines endlichen, dreidimensionalen Objekts, das wir dreidimensionale Sphäre nennen.
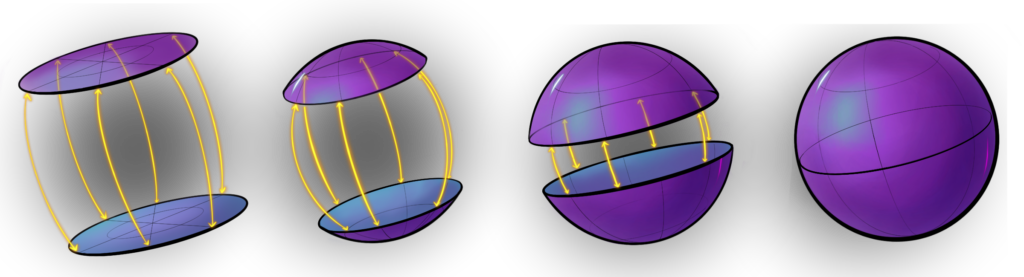
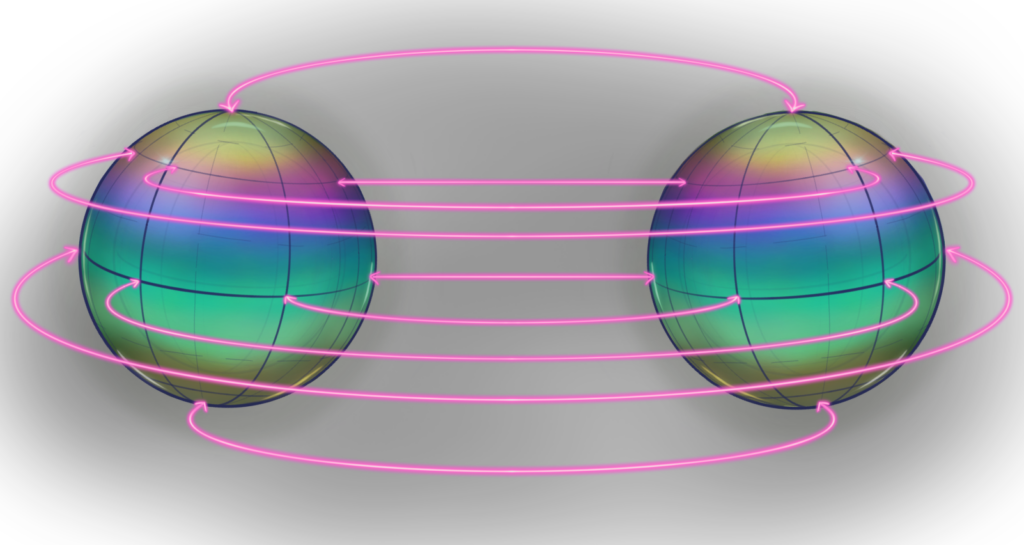
Bemerkenswerterweise hat die dreidimensionale Sphäre auch die Lasso-Eigenschaft, das heißt, sie hat keine Löcher!
Poincaré-Vermutung – ist die dreidimensionale Sphäre besonders?
Ist die dreidimensionale Sphäre das einzige dreidimensionale Objekt mit der Lasso-Eigenschaft? Im Jahr 1904 hat Poincaré die folgende Vermutung aufgestellt:
Ja, die dreidimensionale Sphäre ist das einzige dreidimensionale Objekt mit der Lasso-Eigenschaft!
Henri Poincaré (1904)
Was feiern wir denn nun?
Den endgültigen Beweis der Poincaré-Vermutung! Nachdem sich Mathematikerinnen und Mathematiker fast ein Jahrhundert daran die Zähne ausgebissen haben, wurde die Vermutung 2003 endlich von Grigori Perelman bewiesen. Diese unglaubliche Leistung wurde von ihm erbracht, indem er eine eigentlich noch viel schwierigere Vermutzung bewiesen hat, die sogenannte Geometrisierungs-Vermutung von William Thurston. In dieser allgemeineren Vermutung geht es darum, eine vollständige Liste aller möglichen dreidimensionalen Formen zu erstellen. Auch das ist wieder eine Frage, die analog zum zweidimensionalen Fall gestellt werden kann, aber viel schwieriger ist.
