
Poincaré Conjecture
If it looks like a sphere and feels like a sphere, is it really a sphere?
Science is about understanding phenomena and objects in nature by determining when they are similar and when they are dissimilar. Chemists like to distinguish chemical elements using the periodic table and biologists use the natural characteristics of plants and animals to describe the different species in nature. Similarly, some mathematicians are interested in determining when shapes are alike or dramatically different.
Math surrounds us – in a bakery, a kitchen, a playground…
Here are some objects from everyday life that can be intuitively grouped together according to certain patterns on their surface.

Group 0

Group 1

Group 2

Group 3
All the objects in the pictures are living in a three-dimensional space. If we consider them to be filled (imagine the apple with its peel and pulp), then these are three-dimensional objects. But today we only want to look at the boundary of such an object (now consider only the peel of the apple), this gives us a two-dimensional surface in the three-dimensional space. Here’s now a cute puzzle for you to think about!
Their number of holes! The objects in Group 0 have zero holes, the objects in Group 1 have one hole, and so on.
The intuitive notion of ”having holes” was made mathematically precise by Henri Poincaré around 1895 in his seminal article “Analysis Situs” and his work has had a profound influence on the mathematical field of Topology, which is more generally concerned with the study of space (from the Greek word ”τόπος”=”space”).
The more sophisticated mathematical incarnation of this notion is understood through the so-called “loop-shrinking property”.
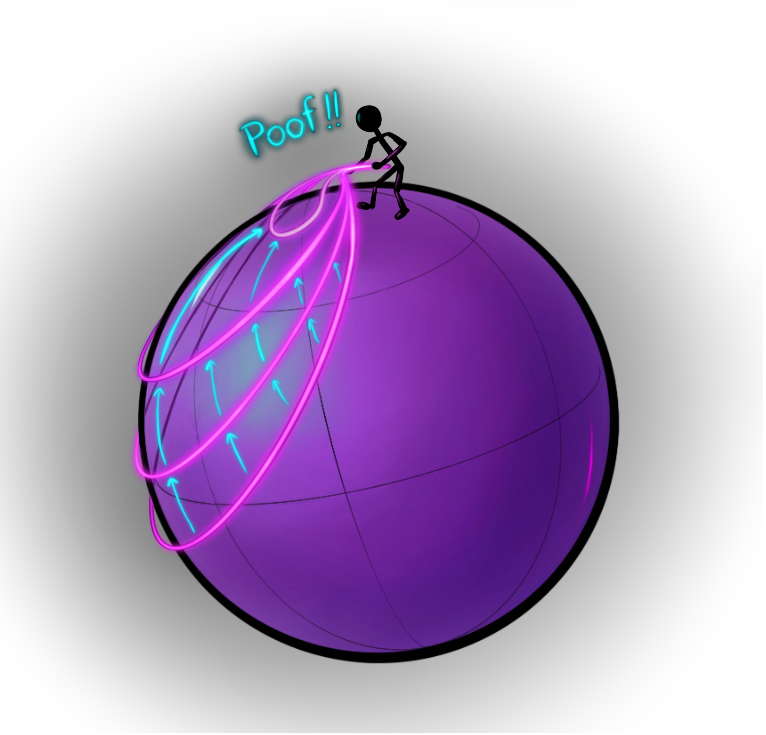

Loop-shrinking Property: Imagine tying an elastic string in a loop around a sphere ( the surface of a ball) and around a torus (the surface of a doughnut), as shown in the pictures on the left.
In the first one, notice that no matter how you tie the string around the sphere, it can always slide off the sphere. However, for the second, we can tie an elastic string in a way that cannot be taken off the torus, unless one either cuts the torus or tears the string.
In fact, all two-dimensional shapes can be distinguished by the number of their holes as in the examples of shapes we have seen above. Mathematically this is very satisfactory because it means that any finite two-dimensional shape can be, in fact, deformed to exactly one with a certain finite number of holes, as in the examples we have seen above. So in topology, a mug and a torus are the same.

Transcending the two-dimensional world …
Can we similarly understand more complicated shapes, like the three-dimensional ones? But what would such an object look like in the first place? Here is one example of a finite three-dimensional object, called the three-dimensional sphere.
Our motivation for the construction comes from the following construction of a two-dimensional sphere: take two 2-dimensional discs and sew or glue their boundary circles, as in the adjoining picture.
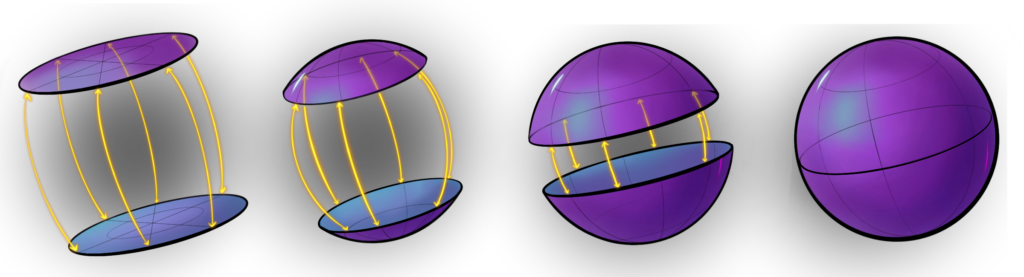
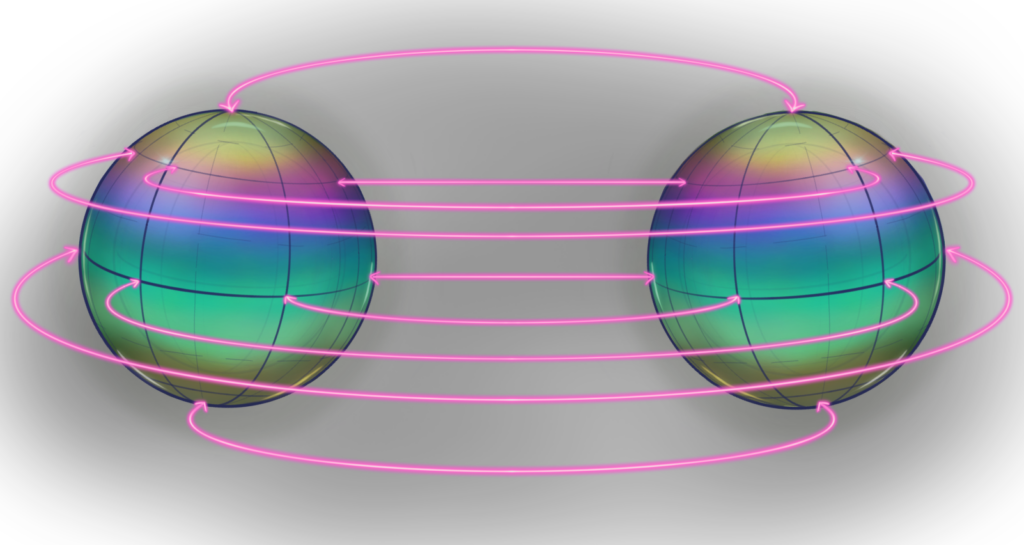
Similarly, a three-dimensional sphere is constructed by taking two three-dimensional discs (imagine, two solid balls of clay) and then gluing their boundary spheres (these are 2-dimensional spheres).
So a person living inside clay ball A can walk to the boundary of ball A, cross over to ball B and keep walking inside ball B. If they keep walking further and reach the boundary of B, they will re-appear inside ball A. Remarkably, note that to such a traveler, the world seems infinite although it is clearly finite as we made it out of two finite pieces.
Notably, the three-dimensional sphere also has the loop shrinking property, that is, it does not have any holes!
Poincaré Conjecture – is the three-dimensional sphere special?
Is the three-dimensional sphere the only three-dimensional object with the loop-shrinking property? In 1904, Poincaré conjectured:
Yes, the three-dimensional sphere is the unique three-dimensional object with the loop-shrinking property!
Henri Poincaré (1904)
What are we celebrating?
We celebrate the resolution of the Poincaré Conjecture! Eluding mathematicians for nearly a century, a rigorous mathematical proof verifying Poincaré’s prediction was finally given in 2003 by Grigori Perelman. This amazing feat was achieved by actually settling an even more ambitious conjecture called the Geometrization Conjecture due to William Thurston. This question concerns developing a complete list of all possible three-dimensional shapes. This is analogous to the case of two-dimensional shapes, where we only had to count the holes.
